สรุปเนื้อหาบทเรียน เรื่อง ระบบจำนวนและการแทนค่าข้อมูลในคอมพิวเตอร์
เลขฐาน
ระบบเลขฐานสอง คือ ระบบตัวเลขที่มีค่าฐานเป็นสอง มีสัญญลักษณ์ 2 ตัว คือ 0 กับ 1 ค่าตามตำแหน่งของส่วนที่เป็นจำนวนเต็มของเลขฐานสอง
ระบบเลขฐานสิบ การเขียนจำนวนในรูปทศนิยมคือการเขียนจำนวนให้อยู่ในรูปเลขฐานสิบ ซึ่งมีสัญลักษณ์อยู่ 10 ตัว (0, 1, 2, 3, 4, 5, 6, 7, 8 และ 9)
|
ระบบเลขฐานแปด เป็นระบบตัวเลขที่มีค่าฐานเป็นแปด มีตัวเลขอยู่ 8 ตัว คือ
0, 1, 2, 3, 4, 5, 6, 7
ระบบเลขฐานสิบหก มีตัวเลขอยู่ 16 ตัว คือ |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
|
การแปลงเลขฐาน 10 ให้เป็นเลขฐาน 8 ทำได้โดยเอาเลขฐานสิบตั้ง แล้วหารด้วยเลข
8 ไปเรื่อย ๆ จนกระทั่งผลลัพธ์เป็น "0" ในการหารนั้นจะต้องเขียนเศษไว้ทุกครั้ง จากนั้นให้
เขียนเศษที่ได้จากการหารโดยเรียงลำดับจากด้านล่างขึ้นด้านบน |
ตัวอย่าง  มีค่าเท่าไรในเลขฐานแปด |
|
ผลลัพธ์ของการแปลง  ให้อยู่ในรูปเลขฐานแปด คือ 
การแปลงเลขฐาน 8 ให้เป็นเลขฐาน 10 ทำได้โดยวิธีการคูณตัวเลขฐาน 8 ในแต่
ละหลักด้วยค่าประจำตำแหน่ง แล้วนำผลลัพธ์ที่ได้มารวมกัน จะได้เป็นค่าของ
เลขฐานสิบ |
ตัวอย่าง มีค่าเท่าไร ในเลขฐานสิบ |
|
ผลลัพธ์ของการแปลง  มีค่าเท่ากับ 
การแปลงเลขฐานสองเป็นเลขฐานแปด |
| จัดเลขฐานสองทีละ 3 ตัว โดยเริ่มจากหลังไปหน้า |
| นำเลขที่จัดได้ แปลงเป็นเลขฐานสิบ |
| เขียนเลขฐานแปดแทนที่เลขฐานสอง เป็นคำตอบที่ได้ |
|
|
ตัวอย่าง  มีค่าเท่าไรในเลขฐานแปด |
|
 มีค่าเท่ากับ 
การแปลงเลขฐานแปดเป็นเลขฐานสอง |
| แปลงเลขฐานแปดให้เป็นเลขฐานสอง เต็มสามหลัก วางเรียงตามลำดับ |
| จากข้อ1เลขฐานสองที่ไม่ครบสามหลักให้ใส่เลข 0 ด้านหน้าให้ครบสามหลัก |
| ค่าที่ได้คือคำตอบเลขฐานสอง |
|
|
ตัวอย่าง มีค่าเท่าไรในเลขฐานสอง |
2 | 5 | 4 | 3 |
10 | 101 | 100 | 11 |
10 | 101 | 100 | 011 |
|
|
มีค่าเท่ากับ 
รหัส BCD-8421(Binary Code Decimal-8421)
เป็นรหัสเลขฐานสอง ขนาด 4 บิต ใช้แทนเลขฐานสิบ0-9โดย 8 4 2 1 คือค่าประจำตำแหน่ง
ของลำดับบิต เช่น 0000-1001
รหัสเกิน 3 (Excess-3 code) เป็นการนำรหัส BCD-8421มาดัดแปลงเนื่องจากรหัส BCD-8421มีค่าได้ตั้งแต่ 0000-1001 รหัสเกิน 3มีค่ามากกว่ารหัสBCD-8421 อยู่ 3
Decimal | BCD-8421 | Excess-3 |
0 | 0000 | 0011 |
1 | 0001 | 0100 |
2 | 0010 | 0101 |
3 | 0011 | 0110 |
4 | 0100 | 0111 |
5 | 0101 | 1000 |
6 | 0110 | 1001 |
7 | 0111 | 1010 |
8 | 1000 | 1011 |
9 | 1001 | 1100 |
|
การคอมพลีเมนต์เลขฐานสอง 1’s complement คือการกลับสถานะของสัญญาณ จาก 0 เป็น 1 และจาก 1 เป็น
0 ทุก ๆ บิต เช่น 1’s complement ของ 1100011 คือ 0011100 2’s complement คือผลบวกของ 1’s complement กับ เช่น 2’s complement ของ
1100011 คือ 0011100 + 1 = 0011101 ซึ่งมีวิธีคิดแบบลัดคือ ให้มองจากบิตต่ำสุด
(ขวาสุด) ไปยังบิตสูงสุด(ซ้ายสุด) หา 1 ตัวแรกให้พบ หากยังไม่พบ ให้คงค่าเดิมเอาไว้
จนกระทั้งพบ 1 ตัวแรกก็ยังคง 1 ไว้ หลังจากนั้นให้เปลี่ยนค่าที่เหลือ จาก0 เป็น 1 และ
จาก 1 เป็น 0 ทั้งหมด
ตัวอย่างที่ 1.22 Binary Number 1’s complement 2’s complement 10101 01010 01011 10111 01000 01001 111100 00011 000100 11011011 00100100 00100101
|
|
|
|
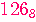
ไม่มีความคิดเห็น:
แสดงความคิดเห็น